Adeus

Caros colegas:

Escrever esse blog e compartilhar nossos estudos com vocês tem sido uma experiencia muito positiva e enriquecedora.

Por meio desse blog, aprendemos muitas coisas, e não apenas sobre os conteúdos da escola. E ficamos muito felizes de termos além disso podido ajudar vocês.

Agradecemos muito a todos os que acompanhavam o blog, e sempre nos incentivaram e apoiaram.

Foi uma decisão difícil, mas nas últimas semanas, escrever nossos resumos se tornou um fardo muito difícil e cansativo, que não nos dava mais a satisfação de antes, mas sim somente desânimo e cansaço, e por isso resolvemos terminar o blog por aqui. Talvez algum dia voltemos a fazer resumos, em um futuro mais distante, mas por enquanto não haverá novas postagens.

Agradecemos a compreensão e o carinho,
Elisa e Maria

Resumo Provão de Física 2º bi

Critérios:

• Queda livre (movimentos verticais)
• Cinemática vetorial
• composição de movimentos

Queda livre (movimentos verticais)

A queda livre o movimento vertical, próximo à superfície da Terra, quando um corpo é abandonado no vácuo ou a resistência do ar é desprezada.
A queda livre é um mruv, sua aceleração é constante e igual a 10m/s², chamada de aceleração gravitacional.
Na queda, o módulo da velocidade do corpo aumenta, o movimento é acelerado, e, portanto, o sinal da aceleração é positivo. Para calcular esse tipo de movimento, as fórmulas são:

h = g . t² /2

v = g . t

v² = 2g∆h

Quando o objeto é lançado para baixo, o movimento da queda vai ser semelhante ao do abandon, porém terá uma velocidade inicial, que lhe dará mais velocidade. A fórmula então precisa considerar isso:

h = h0 + v0.t + g . t² /2

v = v0 + g . t

v² = v0² + 2g∆h

Podemos ver que essas fórmulas são iguais às do mruv normal, apenas com as mudanças de que S foi trocado por H e A por G. Então na verdade não são fórmulas novas para decorar.
Para o lançamento vertical, a aceleração da gravidade, ao invés de aumentar a velocidade, diminui-a, portanto o movimento é retardado. As fórmulas utilizadas serão as mesmas do lançamento para baixo, mas a aceleração da gravidade terá sinal negativo.

Vetores
Vetor é a representação matemática feita através de uma seta, com o objetivo de indicar a medida que ele representa.
Todo vetor é composto por módulo, direção e sentido.
A força é uma grandeza vetorial, pois não basta saber o seu número, também é preciso saber a direção e o sentido em que ela é aplicada.

As operações com vetores são as seguintes:

Vetores com mesma direção e sentido:

4↖  e  5↖. Ambas as forças têm a mesma direção, então são somadas. Total = 9↖

Vetores com mesma direção porém sentidos diferentes.

3→   5→     7←. O total será a diferença entre os lados. Há duas forças indo para a direita, 5 e 3, o total é 8. Uma força vai para a esquerda, 7. A diferença entre os lados é 1, e como as forças para a direita têm módulo maior, a seta será para a direita, então a resposta é 1→. Não existe vetor negativo, o que muda é só a direção da seta!!!

Vetores com direção e sentido diferente (perpendiculares)

Fazer pitágoras para descobrir a resultante:

5↑   12→ 

5² + 12² = fr²

25 + 144 = fr²

169 = fr²

13 = fr

Vetores com ângulos: Somar todas as horizontais e todas as verticais. Depois descobrir a horizontal e a vertical da força com ângulo por meio de seno e cosseno.

Considere que f2 tem ângulo de 30º. Se a força 1 valer 4, a 2 valer 5 e a 3 valer 8 , quanto valerá a resultante?

A força 1 vale 4 no sentido vertical para baixo. A 3 vale 9 no sentido horizontal para a esquerda.

A força 2 é especial. Por estar na diagonal, ela vai para a horizontal e vertical ao mesmo tempo. O seu valor vertical é dado por seno . valor da força, e o seno de 30 é 0,5, então 0,5 . 5 = 2,5 para a vertical para cima. O valor horizontal é cosseno 30 . força. O cosseno de 30 é aproximadamente 0,9, então a força 2 tem valor horizontal de 4,5 para a direita.
Somando as verticais, tem-se 4 para baixo e 2,5 para cima, totalizando 1,5 para baixo.
Somando as horizontais tem -se 8 para a esquerda e 4,5 para a direita, então é 3,5 para a esquerda.
Agora temos uma direção horizontal de 1,5 e uma vertical de 3,5. Elaa são perpendiculares, e para descobrir a resultante é preciso ainda fazer pitágoras.
1,5² + 3,5² = fr²
2,25 + 12,25 = fr²
14,5 = fr²
3,8 = fr

Composição de movimentos
Composição de movimentos é aplicação prática do estud de vetores, com a soma de vetores em situações de vetores, em que mais de uma força influencia um movimento. São problemas para resolver com base no conhecimento sobre os vetores (que já estão explicados acima). Um exemplo clássico é o do barco, que faz um movimento diferente conforme a direção do rio que navega. Ler mais no livro p. 89 a 92.

Bons estudos!!

Resumo Simulado de Química 2º bi

Critérios:

• Distribuição eletrônica em átomos neutros e íons.
• Números quânticos.
• Tabela periódica (posicionamento dos átomos e principais famílias).
• Propriedades periódicas dos elementos (raio atômico e energia de ionização).

Distribuição eletrônica de átomos neutros e íons
A distribuição dos elétrons em camadas na eletrosfera é feita utilizando o diagrama de Linus Pauling.

Podemos perceber que nesse diagrama, os elétrons ocupam camadas mais distantes sem antes terem ocupado completamente as mais internas. Por exemplo, o subnível 4s² vem antes do 3d¹º, apesar de estar na camada de número maior.
Para fazer a distribuição, a regra é a seguinte: Primeiro deve-se verificar quantos elétrons o átomo possui. Sempre se começa pelo menor nível de energia (1s²). Nunca se deve ultrapassar o máximo de elétrons permitido em cada subnível. Quando um subnível estiver totalmente preenchido, passar para o próximo.
Três conceitos são muito importantes. Camada de Valência é a última camada utilizada na distribuição, e é uma das letra K, L, M, N... Subnível mais energético é o último subnível utilizado, por exemplo, 6s², ou 4s². O elétron mais energético é o último elétron distribuído. ATENÇÃO: Nem sempre a camada de valência corresponde ao subnível mais energético (ver exemplo do livro p. 76 e exemplo do CA p.216)

Os íons possuem uma distribuição eletrônica um pouco diferente. Para realizar essa distribuição deve-se primeiro fazer a distribuição dos elétrons no estado fundamental (neutro), e depois retirar/colocar os elétrons que foram modificados na forma iônica.
ATENÇÃO: Os elétrons devem ser adicionados/retirados da última camada (camada de valência), que não necessariamente corresponde ao último subnível da distribuição (subnível mais energético). Ver os exemplos das págs. 77 e 78 do livro.

Números quânticos
Os números quânticos indicam a região de máxima probabilidade de se encontrar um elétron. Cada número indica um dado que ajuda a encontrá-lo.
Número quântico principal (n): É o número que indica em qual camada /nível de energia o elétron se encontra. Como existem 8 camadas (K, L, M, N, O, P, Q, R), o número quântico N varia de 1 a 8.
Número quântico secundário/azimutal (l): Indica o subnível  em que o elétron se encontra (s, p, d ou f). Para o subnível s, é atribuído o valor 0, e nos outros subníveis os valores são 1 até 3.
Número quântico magnético (m): Indica o orbital do elétron (orbital é uma divisão do subnível),

Deve-se distribuir os elétrons, da esquerda para a direita, um por quadrado até o fim e depois recomeçar (máximo 2 elétrons por quadrado). O orbital em que for colocado o último elétron é o número m ( cada quadrado tem um número, conforme a tabela.

Número quântico spin (s): Se refere ao sentido de rotação do elétron, portanto pode ser positivo ou negativo. O valos é 1/2, portanto é -1/2 ou +1/2. Existe a convenção de que o 1 elétron do orbital tem seta para cima e valor de spin negativo, e o segundo do orbital será positivo.

Ver exemplo do livro p. 81.

Organização da tabela periódica
A tabela periódica organiza os elementos químicos em ordem crescente de número atômico. A Tabela Periódica é organizada da seguinte forma:

Colunas Verticais: são as chamadas famílias (divididas em A e B, sendo oito de cada) ou grupos (numerados de 1 a 18); Os elementoos da mesma família possuem semelhança entre suas propriedades.
Família 1A (Grupo 1): Metais Alcalinos
Família 2A (Grupo 2): Metais Alcalino-Terrosos
Família B (Grupo 3 à 12): Metais de Transição
Família 3A (Grupo 13): Família do Boro
Família 4A (Grupo 14): Família do Carbono
Família 5A (Grupo 15): Família do Nitrogênio
Família 6A (Grupo 16): Calcogênios
Família 7A (Grupo 17): Halogênios
Família 0 ou 8A (Grupo 18): Gases Nobres

Colunas Horizontais: são os chamados períodos. Ao todo na tabela, eles são sete.
A partir do período, nós conseguimos determinar o número de níveis de um átomo de qualquer elemento. O subnível mais energético e o número de elétrons podem ser identificados facilmente pela família.

Se o subnível for s ou p, o número do subnível será o do período. Se for d, o número deve ser somado a 1, e se for f, +2. Exemplo: O átomo de ferro (número atômico = 26) tem a seguinte distribuição eletrônica nos subníveis em ordem energética: 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d⁶. Se o seu ultimo subnível é 3d⁶, o período será 3 + 1 =4.

Propriedades periódicas dos elementos (raio atômico e energia de ionização)
O raio atômico (r) éa distância (d) do núcleo de um átomo até o fim de sua eletrosfera. Neste caso, considera-se o átomo como uma esfera. O raio atômico aumenta conforme o número de camadas eletrônicas. Quando dois átomo tiverem o mesmo número de camadas, o maior raio será daquele que tiver o MENOR número de elétrons na última camada.

A energia de ionização é a quantidade de energia necessária para retirar um elétron do átomo, geralmente o último.

Quando os elétrons estão próximos do núcleo, a atração é mais forte, então é mais difícil retirá-los do núcleo. Portanto os elétrons de menor número atômico têm maior energia de ionização. E os elementos da esquerda têm tendência a perder elétrons e os da direita a ganhar, então a energia de ionização dos elementos da direita é maior. 

Bons estudos!

Resumo BJTÃO de Química 1ºbi

Critérios:

• Obtenção de substâncias puras com base em misturas e métodos de separação.
• Estudo da evolução dos modelos atômicos.
• Interpretação dos experimentos que levaram à formulação dos modelos atômicos.
• Átomos neutros e íons.
• Igualdades químicas.
• Distribuição eletrônica de átomos neutros e íons.
• Números quânticos.
• Tabela periódica (posicionamento dos átomos e principais famílias). 

Métodos de separação de misturas

Há uma enormidade de métodos diferentes para a separação de misturas, e como são muitos, aqui serão colocados resumidamente, mas estão explicados de forma mais detalhada no livro de química páginas 34 até 39. 

A - Métodos para separar misturas sólido-sólido heterogêneas

1- Catação: Separar dois sólidos manualmente. Exemplo: Escolher feijão

2- Levigação: Usar uma corrente de água para separa os sólidos. O mais leve é arrastado pela correnteza, e o mais pesado se mantém no lugar. Exemplo: separar ouro de areia no garimpo.

3- Flotação: Usar um líquido com densidade intermediária entre a dos dois sólidos para separá-los. O mais leve flutuará e o mais pesado afundará, possibilitando a separação. Exemplo: Separar serragem e areia

4- Peneiração: Usar uma peneira para separar sólidos de tamanhos diferentes. Também pode ser usado para separar uma mistura de um sólido com um líquido. Exemplo: escorrer macarrão.

5- Dissolução fracionada: Quando um sólido é solúvel na água e o outro não, pode-se usar o método. Adiciona-se água à mistura, depois se filtra e após a água é evaporada. Exemplo: sal (solúvel) e areia (não-solúvel)

6- Imantação/separação magnética: Usado quando um dos sólidos é atraído por ímãs.

7- Fusão fracionada:Separar sólidos com pontos de fusão diferentes. Exemplo: Reciclagem de metais

8- Ventilação: Para misturas com massas bem diferentes, uma é carregada pelo vento do ventilador, e a outra permanece no lugar.

9- Sublimação fracionada: Funciona da mesma forma que a fusão fracionada, com a diferença de que uma das substâncias tem a propriedade de se sublimar.

10- Cristalização fracionada: Ocorre quando dois sólidos estão em um líquido em que ambos se dissolvem, como sal e açúcar na água. O aquecimento ou resfriamento fará com que um deles cristalize e o outro não, já que possuem propriedades diferentes.

B- Métodos para separar misturas sólido-líquido heterogênenas

11- Filtração: Método parecido com a peneiração, porém o filtro consegue reter partículas bem menores. Exemplo: Passar café.

12- Decantação: Aguardar até que os componentes da mistura se separem pela diferença de densidade, um se acumulando no fundo do recipiente ou boiando. Exemplo: Nas estações de tratamento de água, é usado para remover os resíduos sólidos da água.

13- Centrifugação: É uma decantação forçada, para misturas com densidades muito próximas, que demorariam muito para decantar naturalmente. Exemplo: Exame de sangue.

C- Outros métodos de separação de misturas heterogêneas:

14- Decantação entre líquidos: Com funil de decantação, retira-se o líquido que está em baixo e se deixa o que está em cima, devido à diferença de densidades. Exemplo: Separar água e óleo

15 Separação de gasoso e sólido: Filtração de um gás para extrair as pequenas partículas sólidas. Exemplo: Aspirador de pó.

16- Decantação entre sólido e gasoso: Devido à diferença de densidade, o sólido acaba se depositando abaixo do gasoso. Exemplo: Formação de poeira em cima dos móveis.

D- Métodos de separação de misturas homogêneas

17- Fusão fracionada: Assim como para misturas heterogêneas, funciona para as homogêneas também. Exemplo: separação de ligas metálicas.

18- Evaporação: Deixara a mistura em ambiente aberto até que o líquido evapore, para deixar o sólido no recipiente. Exemplo: Obtenção de sal marinho.

19- Destilação simples: Funciona como a evaporação, mas é feita com um aparelho especial, de modo que o líquido evaporado é condensado, assim ele não é perdido.

20- Destilação fracionada: Como a simples, porém para 2 líquidos ou mais. O líquido com menor ponto de ebulição evapora primeiro, e é recolhido. Exemplo: Separação dos componentes do petróleo.

21- Liquefação fracionada: Para misturar de gases, ao resfriar a mistura lentamente, eles vão um a um se tornando líquidos, e aí podem ser separados pela liquefação fracionada. Exemplo: Separação dos componentes do ar.

Sugestão de exercícios: CA p. 175 até 178, 33 até 43 (gabarito no site)

Modelos atômicos

A primeira ideia de átomo na história surgiu na Grécia, criada por Demócrito e outros filósofos gregos, e tinha a concepção filosófica do átomo como sendo uma bolinha maciça e indivisível.

Dois mil anos depois, John Dalton elaborou o primeiro modelo atômico embasado em experiências. Assim como os filósofos, ele acreditava que o átome é indivisível, o que hoje sabemos que é incorreto, mas ele propôs muitas teses que são verdadeiras até hoje. Também propôs uma maneira de representar os átomos que facilita a compreensão do que são substâncias simples, compostas e misturas.

J. J. Thomson, em 1897, descobriu os elétrons, mostrando assim, que o átomo era divisível. Segundo seu modelo, o átomo seria como um pudim de passas, uma bolinha maciça com pontinhos incrustados. 

Rutherford, por meio de seu experimento com uma lâmina de ouro, descobriu que o átomo não era uma esfera maciça, e que possui mais espaços vazios do que preenchidos.

Bohr aperfeiçoou o modelo atômico de Rutherford, porém sem desmentir nada do que ele havia proposto. Em seu modelo, o átomo possui um núcleo pequeno e com cargas positivas, e é circundado pelos elétrons, que possuem órbitas circulares. Ele descobriu que haviam sete camadas diferentes :K, L, M, N, O, P e Q (hoje sabe-se que há oito), e que cada camada tem um número fixo de máximo de elétrons que pode conter.

Sommerfeld complementou o estudo de Bohr, mostrando que os níveis de enegia podiam ainda ser divididos em subníveis, chamados s, p, d, f.

De Broglie propôs que os átomos se comportam ora como partícula e ora como onda, no chamado princípio da dualidade.

Heisenberg demonstrou que é impossível determinar, no mesmo instante a velocidade e a posição do elétron, o chamado princípio de incerteza.

Schrödinger dividiu cada subnível s, p, d, f em om orbitais, qu eseriam a região mais provável de se encontrar um elétron. Cada orbital contém 2 elétrons com spins (rotações) contrários.

Linus Pauling criou a forma mais aceita de explicar a distribuição dos elétrons na eletrosfera conforme sua energia. Eis o seu diagrama:

Experimentos que levaram à formulação dos modelos atômicos

A teoria de Dalton foi baseada principalmente nas Leis Ponderais (livro p. 51), e em alguns experimentos rudimentares, pois na época ele não possuía equipamentos modernos para provar suas teses.

A teoria de Thomson foi baseada em um experimento que utilizava uma ampola de Crookes (tubos de vidro fechados com um eletrodo positivo e outro negativo) contendo gases a pressões extremamente baixas fez uma descoberta imprescindível para a evolução do modelo atômico.

Ele submeteu estes gases a voltagens elevadíssimas, desse modo foi possível observar o aparecimento de emissões, os raios catódicos. Em seguida, foi colocado um campo elétrico externo e, por fim, verificou-se que o feixe de raios catódicos era desviado, sempre indo na direção e sentido da placa carregada positivamente. Portanto, estas emissões possuíam cargas negativas.

Outro ponto importante é que não importava o gás utilizado, sempre ocorria o mesmo; assim Thomson chegou à conclusão lógica de que estas cargas negativas estavam presentes em toda e qualquer matéria, eram parte integrante destas. Desse modo, provou-se que, ao contrário do que Dalton havia afirmado, o átomo não era indivisível, pois possuía uma partícula subatômica negativa, que ficou denominada elétron.

O experimento de Rutherford teve como conclusão o fato de que o átomo tem muito mais espaços  vazios do que matéria propriamente dita.
Para provar que os átomos não são maciços, Rutherford bombardeou com partículas alfa (provenientes de uma amostra do polônio, que é radioativo) uma fina placa de ouro. Ele notou que a maior parte dessas partículas atravessava a lâmina, e pouquíssimas eram repelidas ou desviadas. O motivo de algumas partículas serem repelidas é porque bateram de frente com o núcleo atômico do ouro. As que sofreram desvio passaram muito perto do núcleo, pois a partícula alfa é de carga positiva, e o núcleo do ouro também.
Assim, a Experiência de Rutherford provou que o átomo possui um grande vazio, um espaço muito grande entre os elétrons e o núcleo.

Bohr foi o cientista que descobriu a existência das camadas de energia (K, L, M, N, O, P, Q) onde os elétrons se distribuem. Para fazer essa descoberta, ele primeiramente concluiu que um gás emitia luz quando uma corrente elétrica passava nele. Portanto, os elétrons absorvem energia elétrica e depois a liberam na forma de luz. Com isso, ele deduziu que um átomo tem um conjunto de energia disponível para seus elétrons. Esse conjunto de energias quantizadas mais tarde foi chamado de níveis de energia. Mas se um átomo absorve energia de uma descarga elétrica, alguns de seus elétrons ganham energia e passam para um nível de energia maior, nesse caso o átomo está em estado excitado.

A experiência de Bohr foi o "teste da chama", em que ele verificou o espectro luminoso de cada átomo quando aquecido. Conforme a coloração da chama, pode-se comprovar que cada salto de camada ocorre com uma determinada energia

Sugestão de exercícios: Livro p. 61 e 62 ex. 1 a 10 (gabarito no final do livro)

Átomos neutros e íons

Os átomos são neutros, pois têm número de caragas positivas (prótons) e cargas negativas (elétrons) igual, então estão em equilíbrio. Porém, os átomos têm a capacidade de ganhar ou perder elétrons, ficando com diferença entre prótons e elétrons.Se houver perda de elétrons, o átomo virtará um íon positivo, chamado cátion, e sua carga será +. Se ele ganhar elétrons, se tornará um íon negativo, chamado ânion, com carga -.

ATENÇÃO:

Um íon com carga - possui MAIS partículas negativas, portanto GANHOU elétrons.

Um íon com carga + possui MENOS partículas negativas, portanto PERDEU elétrons.

Igualdades químicas

Isótopos: Possuem o mesmo número de prótons (Z)

Isótonos: Possuem o mesmo número de neutrons (N)

Isóbaros: Possuem o mesmo número de massa (A)

Isoeletrônicos: Possuem o mesmo número de elétrons (E)

Exemplo:

ISÓBAROS

ISÓTONOS

ISÓTOPOS

ISOELETRÔNICOS

Sugestão de exercícios: Livro p. 71 e 72 (gabarito no final do livro)

Distribuição eletrônica de átomos neutros e íons
A distribuição dos elétrons em camadas na eletrosfera ocorre utilizando o diagrama de Linus Pauling.

Podemos perceber que nesse diagrama, os elétrons ocupam camadas mais distantes sem antes terem ocupado completamente as mais internas.. Um dos motivos disso é a repulsão que ocorre entre cargas iguais, afastando os elétrons.
Para fazer a distribuição, a regra é a seguinte: Primeiro deve-se verificar quantos elétrons o átomo possui. Sempre se começa pelo menor nível de energia (1s²). Nunca se deve ultrapassar o máximo de elétrons permitido em cada subnível. Quando um subnível estiver totalmente preenchido, passar para o próximo.
Três conceitos são muito importantes. Camada de Valência é a última camada utilizada na distribuição, e é uma das letra K, L, M, N... Subnível mais energético é o último subnível utilizado, por exemplo, 6s², ou 4s². O elétron mais energético/diferenciação é o último elétron distribuído. ATENÇÃO: Nem sempre a camada de valência corresponde ao subnível mais energético (ver exemplo do livro p. 76 e exemplo do CA p.216)

Os íons possuem uma distribuição eletrônica um pouco diferente. Para realizar essa distribuição deve-se primeiro fazer a distribuição dos elétrons no estado fundamental (neutro), e depois retirar/colocar os elétrons que foram modificados na forma iônica.
ATENÇÃO: Os elétrons devem ser adicionados/retirados da última camada (camada de valência), que não necessariamente é a [ultima da distribuição (subnível mais energético). Ver os exemplos das págs. 77 e 78 do livro.

Sugestão de exercícios: Livro p. 83 ex. 1 e 2.

Números quânticos
Os números quânticos indicam a região de máxima probabilidade de se encontrar um elétron. Cada número indica um dado que ajuda a encontrá-lo.
Número quântico principal (n): É o número que indica em qual camada /nível de energia o elétron se encontra. Como existem 8 camadas (K, L, M, N, O, P, Q, R), o número quântico N varia de 1 a 8.
Número quântico secundário/azimutal (l): Indica o subnível  em que o elétron se encontra (s, p, d ou f). Para o subnível s, é atribuído o valor 0, e nos outros subníveis os valores são 1 até 3.
Número quântico magnético (m): Indica o orbital do elétron (orbital é uma divisão do subnível),

Deve-se distribuir os elétrons, da esquerda para a direita, um por quadrado até o fim e depois recomeçar (máximo 2 elétrons por quadrado). O orbital em que for colocado o último elétron é o número m ( cada quadrado tem um número, conforme a tabela.

Número quântico spin (s): Se refere ao sentido de rotação do elétron, portanto pode ser positivo ou negativo. O valos é 1/2, portanto é -1/2 ou +1/2. Existe a convenção de que o 1 elétron do orbital tem seta para cima e valor de spin negativo, e o segundo do orbital será positivo.

Ver exemplo do livro p. 81.

Sugestão de exercícios:Livro p. 83 e 84 ex. 3 até 10 (gabarito no fim do livro).



A tabela periódica organiza os elementos químicos em ordem crescente de número atômico. A Tabela Periódica é organizada da seguinte forma:

Colunas Verticais: são as chamadas famílias (divididas em A e B, sendo oito de cada) ou grupos (numerados de 1 a 18);

Família 1A (Grupo 1): Metais Alcalinos
Família 2A (Grupo 2): Metais Alcalino-Terrosos
Família B (Grupo 3 à 12): Metais de Transição
Família 3A (Grupo 13): Família do Boro
Família 4A (Grupo 14): Família do Carbono
Família 5A (Grupo 15): Família do Nitrogênio
Família 6A (Grupo 16): Calcogênios
Família 7A (Grupo 17): Halogênios
Família 0 ou 8A (Grupo 18): Gases Nobres

Colunas Horizontais: são os chamados períodos. Ao todo na tabela, eles são sete.
A partir do período, nós conseguimos determinar o número de níveis de um átomo de qualquer elemento. O subnível mais energético e o número de elétrons podem ser identificados facilmente pela família.
Se o subnível for s ou p, o número do subnível será o do período. Se for d, o número deve ser somado a 1, e se for f, +2.

Bons estudos!

Resumo BJTÂO de Física - 1º bi

Critérios:

• MRU
• MRUV
• Gráficos MRU
• Gráficos MRUV

MRU

São os movimentos executados em linha reta e com velocidade constante, como um carro se movendo em uma estrada reta sempre na mesma velocidade.

Antes de calculá-los é importante saber classificá-los. Os progressivos se movem para frente e têm velocidade positiva. Os retrógrados se movem para trás e têm velocidade negativa.

Sua fórmula é:

S= S₀  + v.t

S é a posição no final do movimento, e S₀  é a posição inicial, onde o movimento começou. A velocidade. o tempo e a posição devem estar no mesmo sistema, Se v estiver em km/h, S deverá estar em km e t em horas. Se v estiver em m/s, S estará em metro e t em segundos.

Exemplo: Um carro inicia um movimento no km 70 de uma estrada, e segue até o km 10. Ele faz esse percurso em 30 min. Qual a sua velocidade durante o trecho?

A posição inicial é 70 e a final é 10. Vemos que o carro se move em sentido contrário então o movimento é retrógrado, portanto a velocidade será negativa. O tempo é 30 min, mas como estamos trabalhando com km, deve ser transformado em h, portanto 0,5 h.

S= S₀  + v.t          70 = 10 -v.0,5
                            70 -10 = -v.0,5
                            60 = -v.0,5
                            60:0,5 = -v
                            120 = -v
                             v = 120

Exercícios especiais de encontros:

Qual a posição e o instante do encontro?

Como a distância entre os carros está em km, será necessário converter os valores de velocidade para km/h. Os valores em km/h são sempre maiores do que os em m/s, então devem ser multiplicados. 20 . 3,6 = 72 e 30 . 3,6= 108. Como os carros se movem em sentidos opostos, um das velocidades será negativa.Para esse tipo de problema devem ser feitas 2 equações separadas, uma para cada móvel. Não sabemos a posição final (do encontro) mas sabemos que será a mesma para ambos. A inicial será 0 para um e 300 para o outro. O tempo também não temos, mas sabemos que será o mesmo para ambos.

 A=    S= S₀  + v.t                                          B=     S= S₀ - v.t 

          S= 0 + 72.t                                                    S= 300 - 108.t

Não podemos continuar as equações, pois elas possuem dois valores desconhecidos, então não podem ser resolvidas. Mas sabemos que como as posições iniciais são iguais, podemos substituir uma equação na outra. Assim:

0 + 72.t = 300 - 108.t

72t + 108t = 300

180t=300

5/3 =t

Sabendo que o tempo é 5/3 de hora (1h40min) podemos adicioná-lo às fórmulas. ambas serves, usemos o carro A.

         S= 0 + 72. 5/3

         S= 120

O encontro ocorre 1h40min depois do início do movimento, no km 120 da estrada.

MRUV

Anteriormente, estudamos o Movimento Retilíneo Uniforme, que é reto e com velocidade constante. O MRUV também é reto, mas não é uniforme, sua velocidade varia. Porém a velocidade varia de forma previsível, constante, pois a variação da velocidade (aceleração) é constante.

A grandeza aceração é o quanto a velocidade varia em um espaço específico de tempo (velocidade POR tempo), então é medida em metros POR segundo ao quadrado. O "ao quadrado" é devido ao fato de que a velocidade já é medida em metros POR SEGUNDO, então a aceleração é a variação de velocidade (metros por segundo) por segundo.

A=∆velocidade / ∆tempo

Além de progressivo e retrógrado (para frente ou para trás), os MRUVs também podem ser classificados como:

• Acelerados - se sua velocidade estiver aumentando (se distanciando de 0 - repouso)
•  Retardados - Se sua velocidade estiver diminuindo (se aproximando de 0 - repouso)

Quando a aceleração e a velocidade tiverem o mesmo sinal, o movimento é progressivo. Quando os sinais forem opostos o movimento é retrógrado. Exemplos:

• Um carro está andando a 80km/h quando freia, reduzindo a velocidade em 5km/h². O movimento é progressivo, pois 80 é positivo, e será retardado, pois o carro está freando (se aproximando de v=0, o repouso. Apesar de estar escrito 5km/h², se há uma REDUÇÃO de velocidade de 5km?s², significa dizer que o carro ACELEROU -5km/h², portanto os sinais são opostos, e esse é o porquê de o movimento ser retardado.
• Um carro está andando a  -50km/h, com aceleração de -2km/h². O movimento é retrógrado (está indo para trás) e é acelerado, pois por ser negativa ela impulsiona a velocidade negativa para ir cada vez mais rápido (sinais iguais = acelerado)

Para efetuar os cálculos de MRUV, existem 3 fórmulas:

1. A fórmula da função horária das posições, que é a mesma do MRU, porém com mais um item no final para considerar a aceleração: S = So + Vo . t + at² / 2
2.  A fórmula da função horária da velocidade: V = Vo + a.t
3.  A fórmula de Torricelli: V² =  Vo² + 2a∆S

A equação horária da Velocidade deve ser usada quando o problema não perguntar/ fornecer dados sobre a posição, pois como podemos ver a posição não está incluída na fórmula então não adianta usar. 

A equação do Torricelli deve ser usada quando o problema não perguntar/ fornecer dados sobre o tempo, pois ele não está na fórmula então não adianta usar.

A equação horária da posição pode ser usada para tudo, exceto quando o problema perguntar a velocidade final, que não está na fórmula.

Exemplos resolvidos:

A - Exercícios com fórmula dada: (exercício 10 do livro p. 52, ler o enunciado no livro!)

Essa questão é bem complexa, pois não exige apenas conhecimento das fórmulas, mas também o raciocínio lógico para saber como aplicá-las. 

Primeiramente, sabemos que o que faz um móvel mudar de sentido é a mudança no sinal de sua velocidade, passando de positiva para negativa ou vice-versa. Quando a aceleração faz com que a velocidade vá ficando cada vez mais perto de zero (movimento retardado), ela fará o móvel parar quando chegar na velocidade 0 (atingir o estado de repouso) e depois seguir na velocidade com sinal oposto (mudar o sentido). É como se fosse uma estrada em que o carro de repente para e começa a andar em marche ré.

Foi dada uma fórmula (a da função horária da posição), porém logo vemos que ela não serve, pois tem uma incógnita (o tempo, pedido na questão) mas também falta a posição (x), e portanto não serve. Mas podemos descobrir alguns dados.

S =  So + vo.t + at² /2

X = 3 + 12t - 3t²

Sabemos então que a posição inicial é 3, a velocidade inicial é 12 e a aceleração é -6 (foi multiplicada pelo 2 que deveria estar em baixo conforme a fórmula original). A velocidade final será 0, pois é nesse instante que ocorrerá o repouso e a inversão do sentido. Com esses dados podemos montar a fórmula da equação horária da velocidade.

Vf = Vo + a.t

0 = 12 - 6.t

6t = 12

t = 2

Alternativa C

Provavelmente na prova não haverá nenhum exercício de fórmula dada mais difícil do que esse, então se esse exemplo ficou bem claro, acredito que não haverá dificuldades!

B - Exercício de situação problema (sem fórmula dada) - exercício 13 da p. 52 . Ler o enunciado no livro!
Primeiramente, podemos perceber que se há dois dados sendo pedidos no problema, teremos que usar duas fórmulas ou mais.
Os dados que já temos são a velocidade inicial (72km/h), o tempo (6s) e a velocidade após esse tempo, ou seja, a velocidade final (8m/s). A velocidade 72km/h precisa ser convertida para ficar no S.I, que será então 20m/s. Esses 3 dados são suficientes para montar a equação horária da velocidade:

Vf = Vo + a.t

8 = 20 + a. 6

8 - 20 = 6a

-12 = 6a

-2 = a

Sabemos agora que a aceleração é -2, e com ela podemos descobrir os dados que o problema pede (é essencial saber a aceleração, pois ela está presente nas 3 fórmulas). Agora podemos usar a equação de Torricelli para descobrir a variação da posição (a horária da velocidade não seria adequada, pois envolve posição e tempo, e só podemos descobrir uma incógnita por vez).

Vf² = Vo² + 2a∆S

Notem que aqui a velocidade final não será 8, mas já será 0, pois queremos descobrir a variação de posição até a parada total, como pede o problema, não até o tempo 6s.

0² = 20² + 2. -2. ∆S

0 = 400 -4∆S

4∆S = 400

∆S = 100

Sabendo a variação de posição, podemos descobrir o tempo final, com a equação horária da posição. A variação de posição é 100, então colocaremos a inicial como 0 e a final como 100.

Sf = So + Vo.t + a t² /2

100 = 0 + 20.t -2t² /2

100= 20t -t²

t² -20t + 100 = 0

Agora, por soma e produto, sabemos que os números que somados dão 20 e multiplicados dão 100 são 10 e 10. Então o tempo é 10, e a alternativa é A.

Mais explicações sobre a classificação dos movimentos em acelerado e retardado nas páginas 44 e 45 do livro.

Sugestão de exercícios: CA p. 40 até 42.

Gráficos de MRU

Existem dois tipos de gráficos MRU: os que comparam VELOCIDADE-TEMPO  e os que comparam POSIÇÃO E TEMPO. Os de velocidade são uma linha constante, pois a velocidade não varia. Exemplos de gráfico MRU de velocidade.

Em ambos os gráficos, a velocidade está como uma reta constante, ela não varia. No 2º gráfico porém vemos que o móvel percorre cada trecho com uma velocidade diferente, mas ainda assim, são duas constantes. Se calcularmos a área das figuras, saberemos o deslocamento, pois a fórmula do deslocamento é v.t .

O gráfico abaixo é de comparação entre posição e tempo. No MRU, a posição varia, portanto a reta segue em direção para cima ou para baixo. Se fizermos a área, não acharemos nada, mas  podemos descobrir a velocidade dividindo a VARIAÇÃO da posição (Sf - So) pelo tempo, afinal, v= d : t

Sugestão de exercícios: Livro p. 64 ex. 1 até 4. 

Gráficos MRUV
Existem 3 tipos de gráficos para o MRUV. O que compara ACELERAÇÃO - TEMPO, o que compara VELOCIDADE- TEMPO e o que compara POSIÇÃO-TEMPO.

A aceleração é uma reta constante, pois não varia. Se for feita a área da figura, que é o equivalente a multiplicar a por t, se obterá a variação  da velocidade, que é a fórmula V= a.t.

O gráfico de velocidade-tempo é uma reta que não é constante, pois a velocidade varia no MRUV. 

Quando a reta passa pela velocidade 0, significa que houve uma mudança de sentido!!! Ao calcular a área da figura, podemos descobrir o deslocamento. Ao dividir a VARIAÇÃO da velocidade pelo tempo, saberemos a aceleração (no livro isso está escrito como calcular a tangente, mas é a mesma coisa)

O gráfico de posição-tempo é aquele que possui uma parábola, mas ele não foi estudado.

Bons estudos!

Resumo Simulado de Geografia - 1º bi

RESUMO DO SIMULADO DE GEOGRAFIA - 1º BI

O QUE É A CARTOGRAFIA? 

A cartografia é a ciência da representação gráfica da superfície terrestre, tendo como produto final o mapa. Ou seja, é a ciência que trata da concepção, produção, difusão, utilização e estudo dos mapas. Na cartografia, as representações de área podem ser acompanhadas de diversas informações, como símbolos, cores, entre outros elementos. A cartografia é essencial para o ensino da Geografia e tornou-se muito importante na educação contemporânea, tanto para as pessoas atenderem às necessidades do seu cotidiano quanto para estudarem o ambiente em que vivem.

Fonte: http://www.sogeografia.com.br/Conteudos/GeografiaFisica/Cartografia/

• ·         Localização: termo utilizado para determinar a localização exata de algo sobre a superfície da Terra .
• ·         Posicionamento: local onde algo ou alguém está em relação a outras coisas.
• ·         Orientação: indica o caminho a seguir a partir do local em que se encontra.

COORDENADAS GEOGRÁFICAS:

São como no jogo batalha naval. É quando meridianos e paralelos se cruzam, indicando uma localização. De acordo com o site Mundo Educação:

"Coordenadas Geográficas são linhas imaginárias que cortam o planeta Terra nos sentidos horizontal e vertical, servindo para a localização de qualquer ponto na superfície terrestre."

• ·         Paralelos: são horizontais, paralelos ao Equador.
• ·         Latitude: distância em graus entre os paralelos.
• ·         Meridianos: verticais, paralelos à Greenwich.
• ·         Longitude: distância em graus entre os meridianos.

FUSOS HORÁRIOS:

A sucessão dos dias e das noites deve-se ao movimen­to de rotação da Terra. É esse movimento que determina que as horas sejam diferentes nos diversos locais do planeta. Considerando que a Terra executa seu movimento de rota­ção em 24 horas e, ao completar uma volta em tomo de seu eixo, ela completou um giro de 360°, foram estabelecidas faixas terres­tres com a largura de 15° e todos os pontos localizados em determinada faixa têm a mesma hora.

Fonte: https://www.resumoescolar.com.br/geografia/fusos-horarios-e-cartografia-representacao-grafica-escalas-mapas-e-curvas-de-nivel/

É importante não confundir fusos horários e coordenadas geográficas!

ESCALAS:

• ·         Grandes: maiores que 1:20.000. Geralmente representam uma área que não ultrapassa 10km de raio. Os detalhes da realidade são mantidos devido ao menor número de reduções. Possuem maior detalhamento do que as outras.
• ·         Média: entre 1:25.000 e 1:500.000. Utilizadas nas cartas topográficas, em que a superfície é maior. Retrata com fidelidade os objetos naturais ou artificiais da superfície, inclusive a altimetria do terreno.
• ·         Pequena: menores que 1:500.000. Utilizadas para áreas mais extensas. Possuem menor detalhamento, porém possuem maior amplitude de área.

CURVAS DE NÍVEL:

Curva de nível é o nome usado para designar uma linha imaginária que agrupa dois pontos que possuem a mesma altitude. Por meio dela são confeccionados os mapas topográficos, pois a partir da observação o técnico pode interpretar suas informações através de uma visão tridimensional do relevo.

Fonte: mundoeducacao.bol.uol.com.br/geografia/curva-nivel.htm

Resumo do Simulado de Português 1ºbi

Critérios:

• Interpretação de textos.
• Acentuação gráfica (regras de acentuação)
• Ortoépia
• Prosódia

Regras de acentuação

1. REGRA DAS PROPAROXÍTONAS: Essa é bem fácil, todas as proparoxítonas são acentuadas, sem exceção. Exemplo: árvore, plátano, tímpano.
2. REGRA DOS MONOSSÍLABOS: As palavras de uma só sílaba não são oxítonas, paroxítonas nem proparoxítonas, elas são classificadas em tônicas e átonas. As tônicas são pronunciadas de forma mais forte do que as átonas. Geralmente as tônicas têm os papeis mais importantes nas frases, como verbos, substantivos e adjetivos, enquanto as átonas ocupam papéis secundários, como conjunções, artigos ou alguns pronomes. Os monossílabos tônicos são então acentuados quando terminam em A (s), E (s) ou O(s). Exemplo: dê e de -  me dê o meu caderno - posto de gasolina. O 1º é pronunciado de forma forte, o segundo acaba quase desaparecendo, é pronunciado bem baixo ou falar rápido.
3. REGRA DAS OXÍTONAS: Semelhante à dos monossílabos, se acentua as terminadas em A (s), E (s) e O(s), mas também as terminadas em EM ou ENS. (ver exemplos no livro página 52)
4. REGRA DAS PAROXÍTONAS: É o contrário das oxítonas, os finais acentuados nas oxítonas são os que não recebem acento nas paroxítonas. Todos os outros recebem. (ver tabela no livro p.52). É importante lembrar que palavras como "hífen" recebem acento por terminarem em N, mas ao ficarem no plural terminam em ENS, que é da regra das oxítonas, portanto perdem o acento.
5. REGRA DOS HIATOS: Essa regra é superior às outras, independentemente do final da palavra, se a sílaba tônica for um hiato de I ou U sozinho ou com S, será acentuada (Essa regra tem vários problemas, que estão detalhados no box da página 54. Não deixem de ver!!!). Exemplos: Ca-í-da    sa-ú-de    pa-ís 
6. REGRA DOS DITONGOS ABERTOS: Os ditongos abertos são ei, eu e oi quando o E e o Oé pronunciado aberto (é e ó). Eles são acentuados quando aparecerem em oxítonas e monossílabos, mas não em paroxítonas.
7. REGRA DO ACENTO DIFERENCIAL: Serve para que não se confundam duas palavras escritas da mesma forma. Exemplo: Ele não pôde vir ontem, mas hoje ele pode.  Algumas palavras perderam o acento diferencial pelo novo acordo ortográfico, ver o livro p. 55.
8. REGRA DOS VERBOS TER E VIR: Esses verbos recebem acento circunflexo no presente na 3ª pessoa do plural. Exemplo: Eles vêm para a escola de ônibus. Elas têm um grande talento musical. Os verbos derivados, como "conter" e "intervir", são acentuados na 3ª pessoa do singular com agudo e na do plural com circunflexo. Exemplos: O frasco de xampu contém 200 mLs. Quando os alunos fazem bagunça na aula, os professores intervêm.

Observações: Existem alguns casos especiais que devem ser revisados, que estão nas páginas 57 e 58 do livro. Não deixem de ler!

Ortoépia

É o estudo da pronúncia correta dos fonemas. É estudada mais como curiosidade, e é difícil de ser explicada, pois não possui regras claras. As tabelas são encontradas no livro nas páginas 72 a 75.

Prosódia

É o estudo de qual é a sílaba tônica da palavra. Também não possui muitas regras. Tabela na página 76.

Bons estudos! 
Algumas dicas: Fazer os exercícios do CA, das páginas 14 a 18 (exercícios 16 até 30) e conferir o gabarito no site.
Ler o livro nas páginas sugeridas para saber os casos especiais e as particularidades das regras. 

Resumo Simulado de Literatura 1ºbi

Critérios:

• Arte e Literatura
• Gêneros literários
• Denotação e conotação
• Figuras de linguagem
• Funções da linguagem
• Intertextualidade
• Trovadorismo
• Humanismo

Arte e Literatura

A arte e a literatura estão relacionadas devido ao fato de que ambas são formas que o ser humano usa para se expressar. A literatura é a expressão artística que lida com os jogos de palavras. Geralmente na história, arte e literatura possuem o mesmo estilo em épocas equivalentes.

Ler mais no livro p. 8 até 12.

Gêneros literários

• Na Antiguidade Clássica, havia três gêneros literários: lírico, épico e dramático. O gênero lírico era o gênero da expressão de sentimentos e crenças pessoais e temas subjetivos. Esse gênero originou a poesia como é hoje. O gênero épico é uma narrativa. com enredo que geralmente conta uma história de guerras e feitos heroicos. Já o gênero drama era o texto escrito para ser representado no palco, o texto teatral.
• Na atualidade, porém, os gêneros sofreram modificações, e hoje sua classificação é: Poesia: geralmente é expressa em versos e possui conteúdo subjetivo, buscando mais do que apenas o significado das palavras , mas também a musicalidade delas. Gêneros de Narrativa: São três: romance, conto e crônica. O romance é uma narrativa longa, escrita em prosa e que tem um enredo com diversos personagens. Deriva do gênero épico da Antiguidade Clássica. É importante não confundir romance com história de amor. Romântico é um tipo de romance, também pode ser policial, social, ou outros. O conto é uma narrativa ficcional, parecido com o romance, porém bem mais curto. A crônica também é curta e escrita em prosa, mas a diferença é que apresenta fatos reais somados à opinião do autor, portanto não tem objetivo acadêmico. Drama: É o texto teatral, que é escrito de forma que possa ser encenado, como a divisão das falas dos personagens e as rubricas (notas sobre cenário e forma com que a peça deve ser encenada). Outros gêneros menos relevantes são o parenético (sermões religiosos), epístola (carta), oratória, etc.

Denotação e Conotação

Uma palavra é usada no sentido denotativo (próprio ou literal) quando apresenta seu significado original. que é comum, e consta no dicionário. (Para memorizar: Denotativo - Dicionário, ambos começam com D)

O objetivo do sentido denotativo é informar o receptor da mensagem de forma clara e direta, para fins práticos e utilitários. É encontrada em textos informativos, como: jornais, regulamentos, manuais de instrução, bulas de medicamentos, textos científicos, etc.
Já o sentido conotativo (figurado) apresenta diferentes significados, que não são usuaise por isso estão sujeitos a diferentes interpretações. O significado das palavras é ampliado, indo bem além do original, assumindo um sentido figurado e simbólico.

A conotação, diferente da denotação, não é usada para informar de forma clara e concisa, mas para provocar sentimentos no receptor da mensagem, através da expressividade e afetividade que transmite. É encontrada na linguagem poética e na literatura, e também em conversas cotidianas, em letras de música, em anúncios publicitários, etc.

Exemplos:

A brisa suave acariciou-lhe o rosto. (conotativo)

O vento bateu em seu rosto. (denotativo)

Mais exemplos no site:https://www.normaculta.com.br/conotacao-e-denotacao/
Exercício: p. 94 ex. 10 (gabarito no site

Figuras de Linguagem

São as estratégias literárias que um escritor pode usar nos textos para conseguir algum efeito estético ou interpretação. As mais importantes e mais profundamente estudadas são:
Metáfora: Alteração do sentido de uma palavra ou expressão, para um não usual.
Ex.: As estrelas são pequenos diamantes no céu.
Comparação: Segue a mesma lógica da metonímia, mas utiliza o termo "como"
Ex.: A juventude é como um botão de flor.
Metonímia: Substituição de um termo por outro, como autor pela obra
Ex.: Não gostei de ler Ariano Suassuna
Onomatopeia: Palavra para imitar um som.
Ex.: E então... vrummmm... o avião partiu, deixando para trás uma nuvem de poeira.
Eufemismo: Jogo de palavras utilizado para suavizar algo muito negativo ou pesado.
Ex.: "Ele partiu" em vez de "ele morreu"
Sinestesia: Figura de linguagem que mistura sensações de diversos sentidos.
Ex.: Ela sentiu a luz escorrer delicadamente por entre seus dedos.
Anáfora: Repetição de uma palavra ou expressão no início de uma palavra
Ex.: Quando ria, estava triste
Quando chorava, estava feliz
Quando se calava, estava falante
Quando falava, estava pensando
Ironia: Consiste em expressar, de forma intencional, o oposto do que se quer dizer.
Ex.: Uau, você é muito bom em futebol! Nunca vi ninguém com pés tão descoordenados quanto os seus!
Hipérbole: Exagero proposital.
Ex.: Já te disse um milhão de vezes que não gosto quando você se comporta desse jeito!
Antítese: Colocação de palavras ou frases opostas lado a lado.
Ex.;A verdade e a mentira estão sempre juntas.
Paradoxo: Parecido com a antítese, mas enquanto a primeira é uma relação entre palavras opostas, o segundo é entre ideias.
Ex.: Os mesmo braços que serviram de abrigo hoje transmitem solidão.
Personificação (ou prosopopeia): Atribuição de características humanas a seres inanimados.
Com uma piscadela, a lia despediu-se do sol.
Essas são as figuras de linguagem mais comuns, e que foram mais profundamente estudadas. É aconselhável rever o livro p. 25 e 26 para relembrar as outras figuras de linguagem. E só por curiosidade,na língua portuguesa existem mais de 50 figuras de linguagem, então não aprendemos nem a metade!
Exercícios: CA p. 95 a 100.

Funções da linguagem
De acordo com que é o objetivo principal de uma mensagem, ela pode ter diferentes funções. São elas:
FUNÇÃO EMOTIVA/ EXPRESSIVA: A ênfase da mensagem é no emissor dela, e revela a sua opinião e/ou seus sentimentos. Geralmente, está na 1ª pessoa do singular. Está presente em biografias, memórias, poemas, cartas de amor, diários e resenhas críticas.
FUNÇÃO CONATIVA/ APELATIVA/ INJUNTIVA: Seu foco é no receptor da mensagem. É uma tentativa de influenciar quem lê. Essa linguagem é muito usada em propagandas e sermões, mas na página 84 do CA há um exemplo de testo poético em linguagem conativa. Essa linguagem é facilmente identificada pelo uso do imperativo e do pronome "você", para chamar o leitor.]
FUNÇÃO POÉTICA: Seu aspecto mais importante é a mensagem em si, e a construção e estética dela. É a linguagem floreada e bonita de obras literárias, letras de música, e algumas propagandas.

FUNÇÃO METALINGUÍSTICA: Centralizada no código, a linguagem explica ela mesma, como uma poesia que fala de poemas, ou um dicionário.A metalinguagem não tem o objetivo de significar por si, mas sim tem o objetivo de dizer o que o outro significa.

FUNÇÃO FÁTICA: Tem por objetivo testar o canal de comunicação, e estabelecer ou encerrar contato, como por exemplo em uma conversa ao telefone, dizer "alô

FUNÇÃO REFERENCIAL/ DENOTATIVA: Ênfase no referente (de quem se fala). A linguagem é clara e direta, toda no sentido denotativo. Não é expressa a opinião de quem escreve. Essa função é muito empregada em jornais, resenhas, artigos científicos, e serve para informar, dizendo somente fatos do mundo real. 

Exercícios: Rever páginas 87 a 90 do CA.

Trovadorismo

O trovadorismo iniciou no final do século XII, pois foi quando foi escrita a primeira composição em galego-português, o idioma que deu origem ao português.

A literatura desse período era composta basicamente os poemas escritos pelos trovadores para serem cantados.

O contexto das cantigas era o tempo medieval, portanto havia uma forte influência da Igreja no modo que as pessoas agiam e pensavam, e também as relações sociais eram diferentes, baseadas na submissão. As classes sociais eram distantes umas das outras, com uma demarcação muito forte entre clero, nobreza, senhores feudais e vassalos.

As cantigas geralmente falavam sobre os sentimentos amorosos, ou eram sátiras. Os tipos são:

Cantiga de amor: Tem eu-lírico masculino e fala sobre amores impossíveis, geralmente devido à diferença de classes sociais. A amada é idealizada, e o amor demonstrado é respeitoso, e o eu-lírico se dispõe a fazer tudo por ela, na chamada "vassalagem amorosa"

Cantiga de amigo: Nessas cantigas, o eu-lírico é feminino, e fala de seu amado (o amigo), e da tristeza por estar longe dele. Alguns elementos presentes são a natureza (ambiente do campo) e a família.

Cantiga de Escárnio: Utiliza recursos como sarcasmo ou ironia para fazer uma crítica.

Cantiga de Maldizer: São similares às cantigas de escárnio, porém possuem linguagem mais direta e por vezes vulgar.

Outro gênero textual que também ocorre no trovadorismo são as novelas de cavalaria. Esses textos eram histórias de aventuras, cujos heróis eram cavaleiros corajosos que lutavam contra as forças do mal, e que tinham as características consideradas "ideiais" naquele tempo, como fé, castidade, espirito nobre, fidelidade e coragem.

Exercícios: CA p. 111 até 119 (gabarito no site)

Humanismo
O humanismo foi um período da literatura que reflete os acontecimentos da história na transição da Idade Média para o Renascimento.
Ocorreu de  1418 até 1527, e as ideias no período foram de contestar o que antes era tido como verdade absoluta, pregada pela Igreja. O Teocentrismo foi substituído pelo Antropocentrismo, ou seja, passou-se a valorizar menos a religião e os valores espirituais e mais o ser humano e os valores terrenos.
Houveram vários avanços científicos, e foi a época das Grandes Navegações. Uma invenção muito importante para a literatura foi a prensa mecânica, criada por Johannes Gutenberg em 1450, que permitiu maior acesso aos livros pela população. Assim, o ser humano passou a ser mais critico e racional (Racionalismo).

A produção literária do período humanista consiste em:

• Historiografia: Seu principal representante é Fernão Lopes, que deu início à investigação e documentação sistemática dos reinados.
• Poesia Palaciana: Tinha conteúdo semelhante ao do trovadorismo, mas não estava mais ligada à música, pois tinha seu próprio ritmo criado na linguagem, na métrica e na escolha de palavras. Garcia de Rezende publicou o Cancioneiro Geral, em que reuniu as principais obras da poesia palaciana da época.
• Teatro Popular: É representado por Gil Vicente. Seus textos são satíricos (criticam personagens e instituições da época) e ao mesmo tempo são moralizantes (procuram instruir e ensinar valores morais). O traço medieval é a relação com a religião, e as críticas são o traço que mostra a mudança trazida pelo renascimento.

Bons estudos, façam exercícios do CA!

Dica: É importante também revisar o livro O Santo e a Porca, ele será cobrado na avaliação!

Resumo simulado de Matemática - 1º bi

Critérios:

Frente 1:

• Problemas envolvendo conjuntos
• Conjuntos numéricos
• Sistema cartesiano ortogonal
• Produto cartesiano e relação
• Função
• Gráfico de função

Frente 2:

• Arcos notáveis e arcos complementares
• Razões trigonométricas em um triângulo qualquer
• Circunferência: arco, ângulo central e comprimento
• Arcos simétricos
• Seno e cosseno de um ângulo no ciclo trigonométrico

Problemas envolvendo conjuntos:

Para este critério, não há muitas explicações, deve-se fazer exercícios para praticar. Para resolver os problemas, deve-se sempre reunir os dados e em seguida preencher o diagrama começando pelas intersecções e subtraindo-as depois quando for preencher as partes de fora.

Sugestão de exercícios: livro p. 67 a 69 ex. 1 a 14 (gabarito no fim do livro)

Conjuntos numéricos:

Conjunto dos Números Naturais
São todos os números inteiros positivos, incluindo o zero. É representado pela letra maiúscula N.
Caso queira representar o conjunto dos números naturais não-nulos (excluindo o zero), deve-se colocar um * ao lado do N:


N = {0,1,2,3,4,5,6,7,8,9,10, ...}
N* = {1,2,3,4,5,6,7,8,9,10,11, ...}


Conjunto dos Números Inteiros
São todos os números que pertencem ao conjunto dos Naturais mais os seus respectivos opostos (negativos).
São representados pela letra Z:

Z = {... -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}

O conjunto dos inteiros possui alguns subconjuntos, eles são:

- Inteiros não negativos
São todos os números inteiros que não são negativos. Logo percebemos que este conjunto é igual ao conjunto dos números naturais.
É representado por Z+:

Z+ = {0,1,2,3,4,5,6, ...}

- Inteiros não positivos
São todos os números inteiros que não são positivos. É representado por Z-:

Z- = {..., -5, -4, -3, -2, -1, 0}

- Inteiros não negativos e não-nulos
É o conjunto Z+ excluindo o zero. Representa-se esse subconjunto por Z*+:

Z*+ = {1, 2, 3, 4, 5, 6, 7, ...}

Z*+ = N*

- Inteiros não positivos e não nulos
São todos os números do conjunto Z- excluindo o zero. Representa-se por Z*-.

Z*- = {... -4, -3, -2, -1}

Conjunto dos Números Racionais
Os números racionais é um conjunto que engloba os números inteiros (Z), números decimais finitos (por exemplo, 743,8432) e os números decimais infinitos periódicos (que repete uma sequência de algarismos da parte decimal infinitamente), como "12,050505...", são também conhecidas como dízimas periódicas.
Os racionais são representados pela letra Q.

Conjunto dos Números Irracionais
É formado pelos números decimais infinitos não-periódicos. Um bom exemplo de número irracional é o número PI.
Também são irracionais todas as raízes não exatas, como a raiz quadrada de 2 (1,4142135 ...)

Conjunto dos Números Reais
É formado por todos os conjuntos citados anteriormente (união do conjunto dos racionais com os irracionais).
Não fazem parte desse conjunto apenas os números que não existem, como raiz par de número negativo ou fração de denominador 0.
Representado pela letra R.

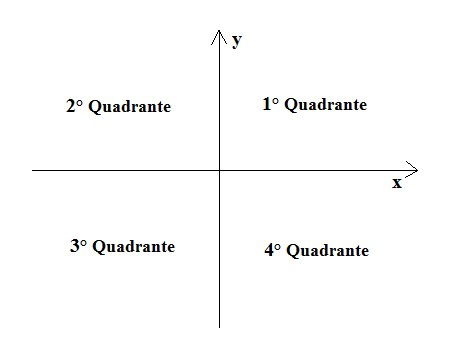
Sistema Cartesiano Ortogonal

Se duas retas se cruzam e formam um ângulo de 90º elas são perpendiculares. A perpendicularidade dessas duas retas forma um sistema cartesiano ortogonal. 
As duas retas são chamadas de eixos: 

Eixo das abscissas: reta x (horizontal)

Eixo das coordenadas: reta y (vertical)

Onde as retas x e y se encontram é formado um ponto, que é chamado de ponto de origem (0,0)
O sistema cartesiano ortogonal é dividido em quatro partes e cada uma é um quadrante. 

Um ponto no sistema cartesiano ortogonal é formado por dois pontos, um do eixo das abscissas e outro do eixo das ordenadas. 
O ponto no sistema cartesiano ortogonal é chamado de par ordenado, como se fosse um jogo de batalha naval

O ponto P possui um número a que é a abscissa do ponto P. 
O ponto P possui um número b que é a ordenada do ponto P. 

(a, b) é chamado de par ordenado do ponto P (sempre primeiro a abcissa e depois a ordenada)

Portanto, para determinarmos um ponto P no sistema cartesiano ortogonal é preciso que as abscissas e as ordenadas sejam dadas. 

Função
Na Matemática, o conceito de função é inteiramente ligado às questões de dependência entre duas grandezas variáveis.
A função f(x) = a + b . x possui um coeficiente fixo (a) e um variável b, que é o n de x. o f(x) variará em função disso.
Exemplo: Ana é vendedora. Seu salário é de R$ 800 fixos + 5% do valor que ela vender. Podemos representar isso como uma função:

f(x) = 800 + 0,05. (x)

Se Ana vender em um mês um total de R$ 5000, qual será seu salário?

f (x) = 800 + 0,05 . 5000

f (x) = 800 = 250

f (x) = 1150

Arco notável e arcos complementares:

Os arcos notáveis são ângulos cujos senos, cossenos e tangentes são valores importantes na matemática. Eis aqui a famosa tabela.

Nos arcos, podemos notar que é interessante a relação quando eles são complementares (somam 90º). Quando isso acontece, o seno de um é o cosseno de outro, e vice-versa. Além disso, a tangente de um é o inverso da tangente do outro (é só inverter a fração). Isso é facilmente observável em 30º e 60º, que têm seno e cosseno opostos e tangentes invertidas (√3 / 3 é na verdade 1/ √3 ,  mas racionalizado)
mas se aplica a todos os complementares.

Razões Trigonométricas em um Triângulo Qualquer
Em triângulos quaisquer (não precisam ser retângulos), o seno de um ângulo vai ser igual ao de seu suplementar (soma 180º), e o cosseno é oposto do suplementar.
Exemplo:

45º e 135º são suplemtentares. 

Sen 45° = √2 /2 e cos 45° = √2 /2

então

Sen 135° = √2 /2 e cos 135° = -√2/ 2

Lei dos senos: A razão dos senos dos ângulos do triângulo com seus lados opostos será sempre igual, e também é equivalente a 2 raios caso o triângulo esteja inscrito em uma circunferência.

Na imagem faltou a relação de = 2r, não esquecer dela!

Exemplo:

Nesse triângulo, montamos a regra de três assim:

90 / sen 45° = x / sen 120°

90 / √2/2 = x / 1/2

90 . 1/2 = x . √2/2

45 = x . √2/2

90 = √2x

90 / √2 = x

45√2 = x

Notem que as duas divisões por 2 já poderiam ter sido cortadas antes!

A lei dos cossenos é mais complexa.

Sua fórmula é:

a² = b² + c² + 2.b.c. cos  (para descobrir b ou c, é só inverter as letras)

Exemplo:

x² = 6² + 10² + 2.6.10. cos 120°

x² = 36 + 100 + 2.60. 1/2

x²  = 136 + 120. 1/2

x² = 136 + 60

x² = 196

x = √196

x = 14

Circunferência: arco, ângulo central e comprimento

O comprimento de uma circunferência é dado em valor de seu raio, conforme a fórmula C = 2 𝛑 r
Exemplo: Uma praça circular tem raio de 40 m. Quantas metros anda uma pessoa quando dá 3 voltas na praça?
C = 2 𝛑 r
C = 2. 𝛑 . 40
C = 80𝛑
80𝛑 é o comprimento da circunferência da praça. Ao dar 3 voltas na praça, será 240𝛑. Usando 𝛑= 3,14 teremos que o comprimento é 753,6 metros, mas a maioria dos exercícios não pede a troca do 𝛑 por 3,14.

O arco de um círculo é uma parte de sua circunferência.
Ângulo central é o ângulo da abertura do arco.
Para calcular a medida do arco e a do ângulo central, usamos  a regra de três. Sabemos que em uma circunferência completa, o ângulo é 360° e a medida da circunferência é 2𝛑 radianos , e 180° tem 𝛑 radianos. Com essas relações podemos resolver os problemas.
Exemplo: um arco tem abertura de 100°. Quantos radianos tem o comprimento desse arco?

Sugiro fazer muitos exercícios, do livro e do CA. Bons estudos!